Lorsque la trajectoire que suit le point 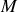est connue il est possible de repérer le point sur la courbe représentant cette trajectoire. On choisit sur la courbe orientée un point origine 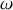et on définit l'abscisse curviligne 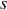comme la mesure algébrique sur la courbe de la distance  :

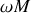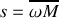(mesure sur la courbe)

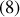
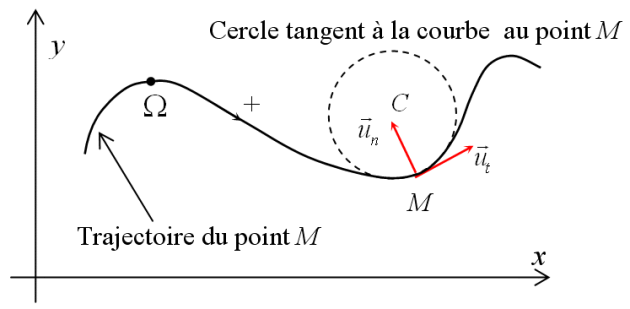
Figure 7 : Abscisse curviligne ( 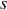= mesure 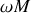sur la trajectoire) et base de Frenet

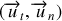
Le cercle de centre 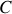et de rayon 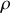qui tangente localement en 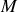la trajectoire du point est appelée cercle osculateur. Le rayon 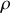de ce cercle correspond alors au rayon de courbure de la trajectoire au point considéré (voir figure 7) et 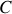est le centre de courbure. En chaque point 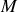de la courbe on définit la base de Frenet 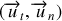avec :

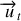 : Vecteur unitaire tangent à la courbe en 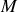et orienté dans le sens positif choisi.

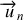 : est un vecteur perpendiculaire à 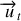, et orienté vers le centre de courbure (de 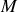vers 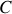). Cette base est "mobile" dans le repère.